Gastautoren 📝 Dieser Beitrag wurde von einem Gastautor verfasst. Interessante Artikel rund um die Themen Finanzen und Investieren teile ich hier auf aktiengram.de. Auf der Seite Gastautoren findet ihr alle bisherigen Artikel. Gastautor werden? Alle Infos dazu findest du auf dieser Seite.
Wie man sich mit Statistiken die Welt so hin rechnet, wie man sie haben will
Unsere moderne Welt ist voll mit Zahlen und Statistiken, alles wird versucht genau zu quantifizieren. Das trifft ganz besonders für Finanzbereich zu – und ist auch notwendig und, für den ein oder anderen, auch eine großartige Sache. Doch da, wo viele Zahlen eingesetzt und Statistiken zitiert werden, kann man auch viel an der Nase herumgeführt werden. Das „Lügen mit Statistiken“ ist nichts Neues, bereits 1954 erschien das Buch „How to lie with statistics*“ in dem Darrell Huff die verschiedenen shady methods beim Arbeiten mit Statistiken beleuchtet. Obwohl schon so lange bekannt, sieht man auch heute immer wieder ein paar Klassiker.
Eine oft genutzte Methode ist die Verzerrung oder unrealistische Darstellung der Achsen einer informativen Grafik. So vor kurzem auf Instagram beobachtet: In einem, hier nicht näher genannten, Post wurde die erwartete Rendite bei verschiedenen Depotkosten verglichen: keine Depotkosten, 1-50 € pro Order, oder 0,3%/0,5% pro Jahr. Um die erhaltenen Werte zu visualisieren, wurde ein Säulendiagramm erstellt, das in etwa so aussah:
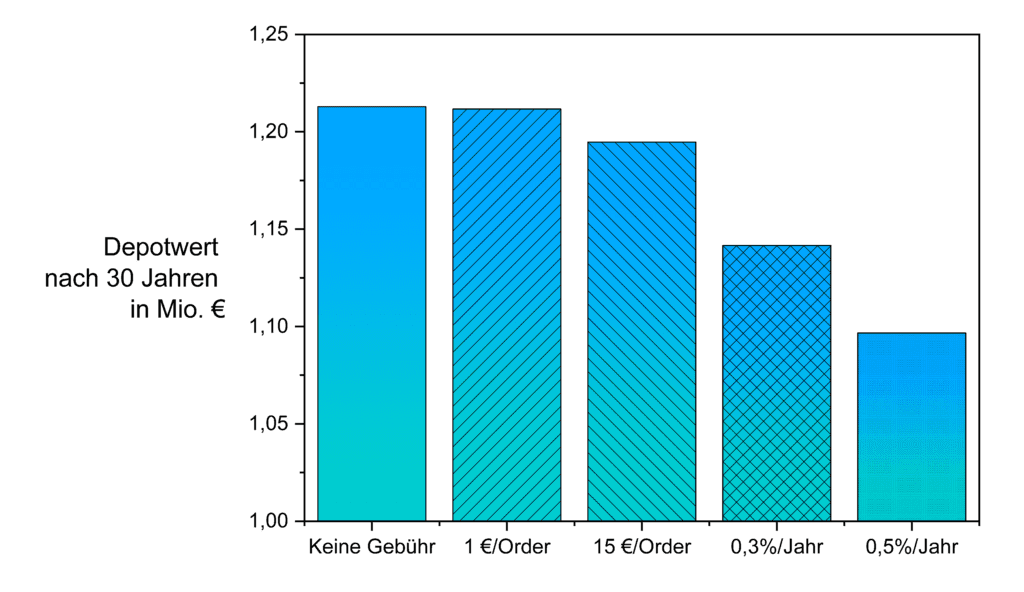
Schaut man sich das Diagramm und die Kosten im eigenen Depot an, läuft es einem kalt den Rücken runter: mit nur 0,5% Gebühren sinkt der erwartete Depotwert auf ungefähr die Hälfte!
Aber kann das wirklich sein?
Betrachtet man das Ganze etwas genauer merkt man, dass der y-Achsenabschnitt – die sogenannte Ordinate – sehr seltsam gewählt wurde. Welche Aussagekraft hat der gewählte Abschnitt von 1-1,25 Mio €? Um es kurz zu machen: keine. Deutlich sinnvoller ist ein solches Diagramm, wenn man sich das Prinzip der Proportionalen Tinte (besser auf Englisch bekannt als principle of proportional ink, kurz PPI) hält. Hierbei muss jede eingefärbte Fläche proportional zur Datenmenge sein, die sie repräsentiert. Das geht ganz einfach bei einem Säulendiagramm: Man setzt den „Anfang“ der Y-Achse auf 0! Das Diagramm von oben sieht dann folgendermaßen aus:
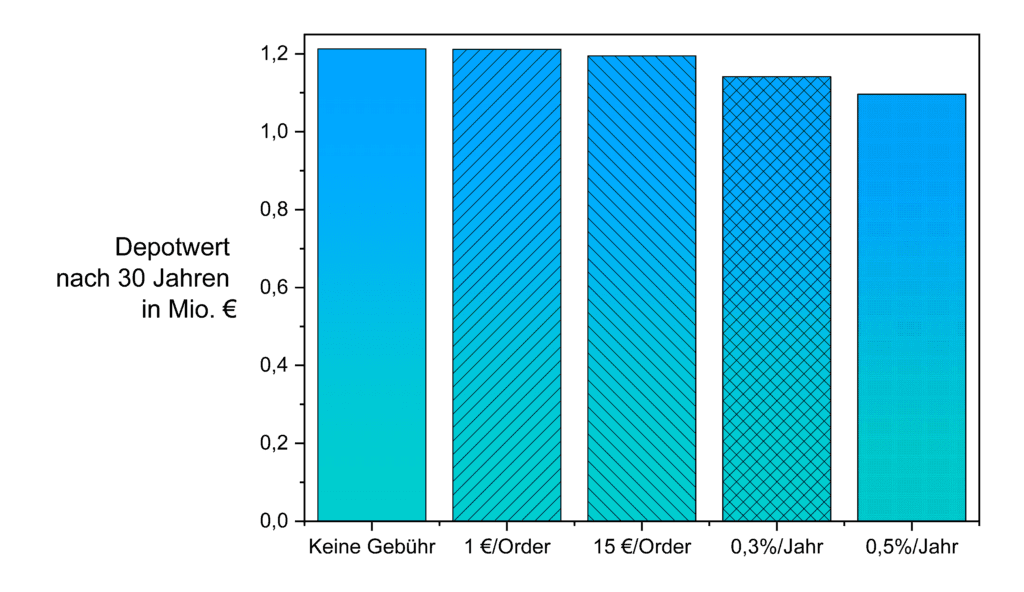
Und tatsächlich, dieses Diagramm vermittelt den tatsächlichen Sachverhalt deutlich besser. Der erwartete Depotwert sinkt im genannten Beispiel von 1,212 Mio. € auf 1,096 Mio. €, also knapp 10%. Das ist in einem Diagramm, das dem Prinzip der proportionalen Tinte entspricht, völlig eindeutig zu erkennen: Die gezahlten Gebühren in diesem Szenario (30 Jahre Ansparphase, 1000 €/Monat Sparbetrag, 7% jährliche Verzinsung, 1 €/15 € Kosten pro Order bzw. 0,3%/0,5% Kosten pro Jahr, Orderkosten und Zinsen jährlich gerechnet, hier sind die Rechnungen zu finden) spielen zwar eine Rolle für die Performance, sind aber lange nicht so dramatisch wie im ersten Beispielgraph gedacht.
Eine weitere beliebte Methode, Zahlen so zu präsentieren, dass ihre Einordnung schwierig ist, ist der „Durchschnitt“: durchschnittlich bekommt eine Frau in Deutschland 1,58 Kinder, durchschnittlich verdient jede*r Deutsche 4100 € brutto pro Monat, durchschnittlich … Eigentlich ist auch das wieder eine nette Sache. Schließlich kann kaum jemand was damit anfangen, dass alle Deutschen zusammen jedes Jahr ca. 45 Mrd. € sparen – ein durchschnittlicher Sparbetrag von 550 € macht das Ganze viel greifbarer. [1] Das Problem ist vielmehr, wie dieser Durchschnitt erhoben wird. In den meisten Fällen wird das arithmetische Mittel gebildet: Dabei werden alle Einzelteile aufsummiert und durch die Anzahl geteilt. Bei dieser Methode werden jedoch wenige große Beiträge gegenüber vielen kleinen Beiträgen stark überschätzt! Doch gerade beim Sparen oder beim Einkommen ist ja gerade das Spannende, was die „Normalos“ so machen.
Das Nutzen des „falschen“ Durschnitts kann dann durchaus verwirren: Wohingegen ein arithmetisch gemitteltes deutsches Einkommen von ca. 4100 € sehr nett klingt, fühlt sich ein Medianeinkommen von 1869 € schon ganz anders an! [2] Der Median ist der Wert, bei dem „oberhalb“ und „unterhalb“ gleich viele Datenpunkte sind – sozusagen die echte Mitte. Das arithmetische Mittel aber wird durch einige wenige sehr große Datenpunkte verzerrt und kann kein realistisches Bild mehr abgeben.
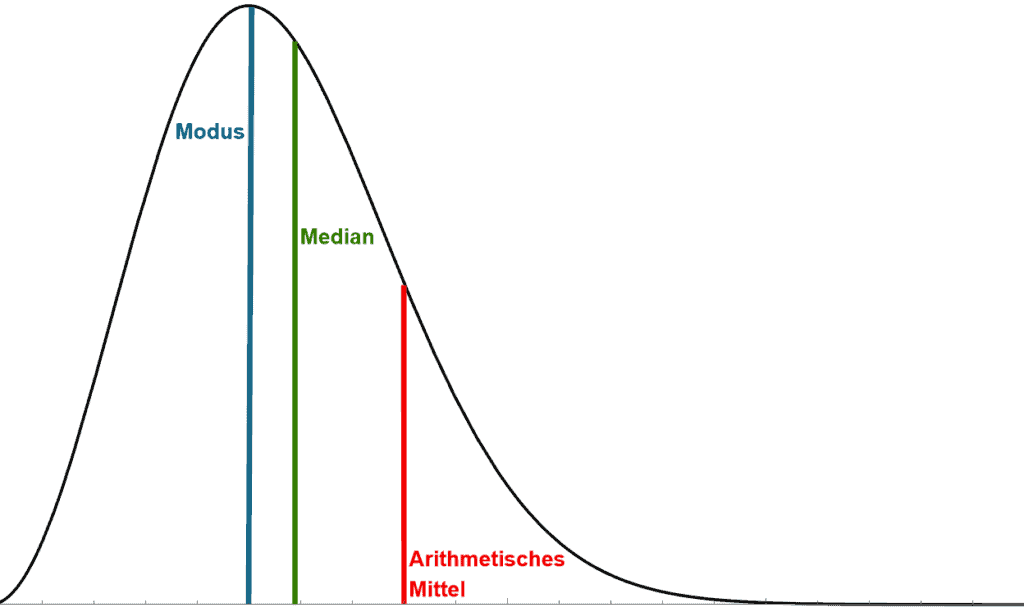
In dieser Grafik ist eine fiktive Verteilungsfunktion, wie z.B. des Einkommens, gezeigt. Das arithmetische Mittel (rot, ganz rechts) und der Median (grün, mittig) werden oft verwechselt. Der Modus, oder besser Erwartungswert, ist der Wert mit der höchsten Eintrittswahrscheinlichkeit/dem höchsten Aufkommen.
So kann man mit verzerrten Darstellungen und „falschen“ Durchschnitten durchaus eine politische Forderung gut untermauern, obwohl, wenn genau betrachtet, die Datenlage diese Forderung nicht zulässt. Im wissenschaftlichen Bereich gibt es hierfür den peer review Prozess: Alle Publikationen werden vor Veröffentlichung von Expertinnen und Experten aus demselben Fachgebiet gegengecheckt – da fällt die meiste Schummelei sofort auf. Doch das ist in der Zeitung kaum und in sozialen Medien quasi gar nicht möglich. Hier bleibt nur: Immer kritisch bleiben.
Hat dir dieser Artikel gefallen oder weitergeholfen?
Wenn du meine Arbeit rund um Aktiengram unterstützen möchtest, freue ich mich sehr über eine Spende an die Aktiengram Stiftung. Mit diesen Geldern unterstütze ich Projekte rund um das Thema Finanzen. Danke fürs Lesen und Mitwirken! ♥️
Übrigens: Spenden über bcause sind steuerlich absetzbar. Deine Einzahlung gilt gemäß § 10b EStG als Spende an die gemeinnützige bcause-Treuhandstiftung. Du erhältst automatisch eine Spendenquittung nach jeder Einzahlung.
Meine eigenen Accounts sind hier verlinkt, darüber hinaus habe ich keine. ⚠️ Passt hier immer auf, auch bei TikTok, WhatsApp und anderen Plattformen gibt es häufig Fake Accounts, die meine Inhalte duplizieren und euch teilweise sogar aktiv anschreiben.
📀 Disclaimer: Das Investieren in Wertpapiere ist mit Risiken verbunden. Ihr handelt immer auf eure eigene Verantwortung! Bitte betreibt dabei immer eure eigene Recherche. Das gilt sowohl für Gebühren, Kennzahlen als auch für die Qualität von Aktien, Anleihen, ETFs und sonstigen Wertpapieren. Die genannten Informationen oder Kennzahlen wurden nach bestem Wissen und Gewissen notiert. Dabei besteht keine Garantie auf Richtigkeit oder Aktualität der Daten. Die genannten Informationen stellen keine Anlageberatung, keine Anlageempfehlung und auch keine Aufforderung zum Kauf oder Verkauf von Wertpapieren oder sonstigen Finanzprodukten dar. Es handelt sich zu keinem Zeitpunkt um eine Anlageberatung, Empfehlung, Steuerberatung oder sonstige fachliche Beratung.
Bei mit Stern (*) markierten Links handelt es sich um Affiliate-Links. Durch Nutzung dieser Links entstehen weder Nachteile noch Mehrkosten. Einige Anbieter ermöglichen dadurch sogar verbesserte Konditionen oder exklusive Boni und Prämien.






Sehr schöner Artikel. Danke.
Wie Grafiken uns wunderschön die falschen Schlüsse ziehen lassen können (sei es bewusst durch den Ersteller geplant oder aus Unwissenheit) hat insbesondere vor einigen Dekaden Edward Tufte gezeigt. Also eine Websuche wert.
Ein guter deutscher Einstieg findet sich hier:
https://www.graphomate.com/2022/08/meine-dataviz-heldinnen-4-5-edward-tufte-der-guru-des-informationsdesigns/
Danke Lisa,
Danke Niko,
für diesen tollen Artikel. Das macht Lust auf ganz viel mehr 😉
Im Prinzip ist es jedem klar „traue keiner Statistik die du nicht selber gefälscht hast“.
Aber oft genug lässt man sich täuschen, wenn man nicht 100%ig bei der Sache ist. Gerade auf der Homepage im IR-Bereich, Geschäftsberichten und bei Unternehmenspräsentationen habe ich das schon so oder so ähnlich erlebt.
Jeden sollte es klar sein, der Job der IR-Abteilungen ist es, Aktien zu „verkaufen“.
Drum Augen auf beim Aktienkauf. 😉
Beste Grüße
Marc
… nicht nur beim Aktienkauf. Traue auch keiner Statistik in den Medien. Wie lautet der letzte Satz in dem sehr guten Gastbeitrag? Immer kritisch bleiben!
Anzeige